Sky Coordinates
by John E. Ross, Univ. of Queensland, Australia
When you want to tell someone where something is on the earth, you could give
the terrestrial coordinates, latitude and longitude. (The altitude
above sea level would be helpful.) There is a similar system for the sky but it
is a bit tricky to use since we are not in the system. In fact, there are two ways
of "pointing" to something in the sky: local systems and sky systems.
The horizon system is centered on the observer and consists of (altitude,
azimuth).
Altitude alt, is an angle measured from the horizon "straight up" to the
object so alt ranges between zero and ninety degrees, 0 ≤ alt ≤ 90°
.
Azimuth az an angle measured eastwards along the horizon from due north
through 360° . Due east is 90° , due west is 270° and halfway up north-by-northwest
is (45° ,330°).
The point directly overhead is called the zenith and astronomers usually
quote zenith distance z=90-alt rather than alt.
Note that the airmass or number of atmospheres a celestial object passes
through is just the secant of the zenith distance and airmass=sec(z)
as long as z is not too large (z<85°).
The great circle that runs from due north through the zenith to due south is
called the local meridian (dashed line in figure below).
A camera or telescope mounting ("tripod") can "point" if it has two axes of rotation.
If the axes are altitude and azimuth the mounting is called "alt-az".
An alt-az mounting is great for looking at terrestrial scenes but the earth's
rotation causes celestial objects to move with time both in altitude and azimuth
at a variable rate making it really difficult to "track" objects. Alt-az coordinates
of an object vary with time and are different for different places on earth.
It is very convenient to consider a system in which only a single coordinate
depends on time. The trick is to tilt the alt-az mounting by an angle equal to (90°-latitude)
towards the celestial pole so the old altitude axis is aligned parallel to the earth's
axis. This polar aligned axis is called the declination or dec axis which
now points toward the celestial pole instead of the zenith. Now once a sky object
is located it can be tracked with a single motion (the old azimuth motion).
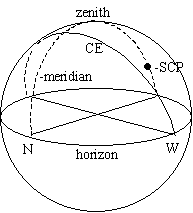 Declination runs from d=+90° at the north celestial pole
through zero at the celestial equator (CE, a projection of the Earth's equator on
to the celestial sphere) to -90° at the south celestial pole (SCP). A given declination
is represented by a small circle of declination on the celestial sphere except for
zero declination, the great circle called the celestial equator. At latitude
f declination d=f is always
on the zenith.
Declination runs from d=+90° at the north celestial pole
through zero at the celestial equator (CE, a projection of the Earth's equator on
to the celestial sphere) to -90° at the south celestial pole (SCP). A given declination
is represented by a small circle of declination on the celestial sphere except for
zero declination, the great circle called the celestial equator. At latitude
f declination d=f is always
on the zenith.
The old azimuth is replaced by (great circles of) hour angle measured
east (or west) of the local meridian. Each hour corresponds to 15° of arc along
the celestial equator. The projection of the local meridian on the celestial sphere
is zero hours. Rising objects are east and setting objects west. Due east on the
eastern horizon (which contains the celestial equator) is six hours east, the western
horizon six hours west. A celestial object with HA 2 hours east (HA=2h00mE) will
cross the meridian in two hours. The ancient astronomers measured this quantity
referred to the rising point on the horizon and called it ascension.
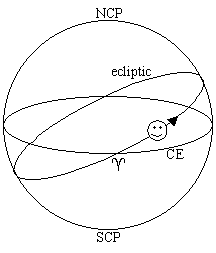 The HA-dec system is what is actually what is used by many observatories and astronomers
but the HA of an object still depends on time and observer location. So the great
circles of HA are fixed on the celestial sphere with the zero point defined as one
of the intersections of the celestial equator and the ecliptic, the vernal equinox
(^). This coordinate is called right ascension
and increases to the east from zero hours at the vernal equinox around the celestial
sphere through 24 hours (360°). RA and HA are both measured in hours (h) minutes
(m) and seconds (s) of time. The sky is divided into 24 hours so each hour corresponds
exactly to 15° of arc (angle), each minute 15' of arc
and each second 15" of arc. One degree of arc corresponds to 4 miutes of time.
The HA-dec system is what is actually what is used by many observatories and astronomers
but the HA of an object still depends on time and observer location. So the great
circles of HA are fixed on the celestial sphere with the zero point defined as one
of the intersections of the celestial equator and the ecliptic, the vernal equinox
(^). This coordinate is called right ascension
and increases to the east from zero hours at the vernal equinox around the celestial
sphere through 24 hours (360°). RA and HA are both measured in hours (h) minutes
(m) and seconds (s) of time. The sky is divided into 24 hours so each hour corresponds
exactly to 15° of arc (angle), each minute 15' of arc
and each second 15" of arc. One degree of arc corresponds to 4 miutes of time.
The sun appears to move eastwards along the ecliptic about a degree (4 minutes
of time) a day and when it crosses the celestial equator moving south to north it
defines zero RA (a=00h 00m 00.0s). RA increases
to the east, the direction the sun moves along the ecliptic through the year.
Now for the hard part. Coordinates on the celestial sphere are RA and DEC but
to know where to "look" for an object in the sky we want the HA and DEC. This is
easy if we know the right ascension that is on the meridian when we look at the
sky. And this is just how sidereal time is defined. Actually, you will hear
the definition local sidereal time is the hour angle of the vernal equinox
but that is the same thing. So if you know the local sidereal time (LST) and RA
then LHA=LST-a (west).
If LHA is negative, or greater than 12, it is usual to convert to "HA East".
So if RA=3h and LST=5h then HA=2h (west), when LST=10h, HA=7h (west), LST=15h HA=12h,
LST=20h HA= 17h(west) or 7h(east), LST=1h HA=-2h (west)
or 22h (west) or 2h (east).
| airmass |
sec(z) |
Amount of atmosphere light traverses. |
| altitude |
alt |
Horizon system coordinate. Zenith=90°
|
| alt-az |
|
Terrestrial telescope mounting or horizon coordinate
system. |
| azimuth |
az |
Angle measured along the horizon eastward from
north. W=270° |
| celestial equator |
x |
Projection of earth's equator on celestial
sphere. |
| declination |
d |
angular distance north or south of the celestial
equator measured along an hour circle. |
| equatorial |
|
pertains to coordinates in which the celestial
equator is a fundamental plane. |
| local hour angle |
LHA=LST-a hour=15°
|
The angle measured to the west of the meridian
along the celestial equator to the circle of RA (hour circle) of an object
expressed in hours. |
| hour circle |
|
A great circle passing through the celestial
poles. A circle of RA. |
| ecliptic |
|
Plane of Earth's orbit. Apparent path of sun
on the celestial sphere. Derives from eclipse. |
| right ascension |
a |
Angle measured eastward along the celestial
equator to the hour circle of an object expressed in hours of time. |
| zenith distance |
z=90-alt |
|
 Declination runs from d=+90° at the north celestial pole
through zero at the celestial equator (CE, a projection of the Earth's equator on
to the celestial sphere) to -90° at the south celestial pole (SCP). A given declination
is represented by a small circle of declination on the celestial sphere except for
zero declination, the great circle called the celestial equator. At latitude
f declination d=f is always
on the zenith.
Declination runs from d=+90° at the north celestial pole
through zero at the celestial equator (CE, a projection of the Earth's equator on
to the celestial sphere) to -90° at the south celestial pole (SCP). A given declination
is represented by a small circle of declination on the celestial sphere except for
zero declination, the great circle called the celestial equator. At latitude
f declination d=f is always
on the zenith. The HA-dec system is what is actually what is used by many observatories and astronomers
but the HA of an object still depends on time and observer location. So the great
circles of HA are fixed on the celestial sphere with the zero point defined as one
of the intersections of the celestial equator and the ecliptic, the vernal equinox
(^). This coordinate is called right ascension
and increases to the east from zero hours at the vernal equinox around the celestial
sphere through 24 hours (360°). RA and HA are both measured in hours (h) minutes
(m) and seconds (s) of time. The sky is divided into 24 hours so each hour corresponds
exactly to 15° of arc (angle), each minute 15' of arc
and each second 15" of arc. One degree of arc corresponds to 4 miutes of time.
The HA-dec system is what is actually what is used by many observatories and astronomers
but the HA of an object still depends on time and observer location. So the great
circles of HA are fixed on the celestial sphere with the zero point defined as one
of the intersections of the celestial equator and the ecliptic, the vernal equinox
(^). This coordinate is called right ascension
and increases to the east from zero hours at the vernal equinox around the celestial
sphere through 24 hours (360°). RA and HA are both measured in hours (h) minutes
(m) and seconds (s) of time. The sky is divided into 24 hours so each hour corresponds
exactly to 15° of arc (angle), each minute 15' of arc
and each second 15" of arc. One degree of arc corresponds to 4 miutes of time.